L'entropie est parfois présentée comme une mesure du désordre. Le but est ici de se convaincre qu'une telle interprétation est en général inadaptée à la compréhension de la nature de l'entropie.

Cet article a pour ambition de permettre au lecteur profane d'appréhender l'idée d'entropie. Une approche mathématique est employée. Cependant, pour l'essentiel du propos, peu de calculs sont en jeu.

D'autres articles discuteront de l'entropie en lien avec des systèmes physiques.

Les résultats de simulations sont utilisés à des fins d'illustration. Les scripts en langage Python de ces simulations sont disponibles ici.

Bonne lecture.

Pile ou Face ?

Utilisons pour commencer un jeu très simple, Pile ou Face.

Lorsqu'on lance une pièce bien équilibrée, on a une chance sur deux de tirer Pile et une chance sur deux de tirer Face. En d'autres termes, la probabilité d'observer Pile et la probabilité d'observer Face sont égales et valent `1/2`.

Que va-t-on observer si on lance une pièce un grand nombre de fois, par exemple 10000 fois, ou si on demande à 10000 personnes de jeter chacune une pièce ?

Réaliser 10000 lancers est une tâche longue et fastidieuse qu'un ordinateur peut effectuer par le biais d'un programme informatique appellé simulation. Par ce moyen, on peut réaliser en une fraction de seconde ce qui prendrait des heures dans la réalité.

Le graphique ci-dessous a été obtenu à l'aide d'une telle simulation de 10000 lancers. Y sont réprésentés le nombre de fois où Pile et Face ont été observés.

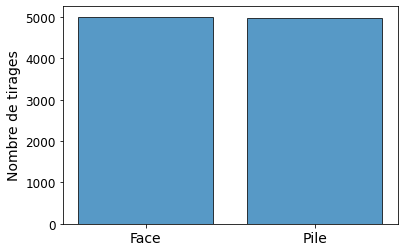
Comme on le voit sur la gauche du graphique Face a été observé 5010 fois dans cette simulation particulière. Sur la droite, on voit que Pile a été observé 4990 fois. Le fait que Pile et Face sont observés dans des proportions très proches provient du fait que chaque lancer de pièce individuel a une probabilité égale d'aboutir à Pile ou Face.

Renouvelons le jeu, mais cette fois-ci en lançant successivement deux pièces et en notant l'ordre des résultats. Quatre observations sont possibles : Pile puis Pile (noté PP), Pile puis Face (noté PF), Face puis Pile (noté FP) et Face puis Face (noté FF).

Si l'on procéde à de multpiles tirages avec deux pièces, mettons 10000, on s'attend à observer PP, PF, FP et FF un nombre similaire de fois. Ces quatre arrangements ayant en effet chacun une chance sur quatre d'être obtenu. On dit qu'ils sont équiprobables, avec la probabilité égale à `1/4`.

Le graphique ci-dessous est là encore le résultat d'une simulation qui a réalisé 10000 tirages avec deux pièces. Il montre le nombre de fois où FF, FP, PF et PP ont chacun été observés.

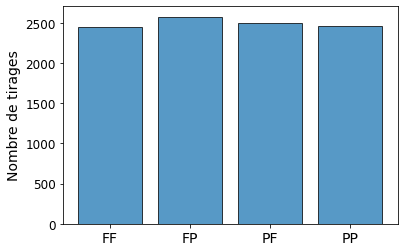
On peut remarquer que chaque arrangement a été obtenu environ 2500 fois, soit près d'un quart du temps, comme le laissait prévoir la probabilité d'une chance sur quatre.

Dans l'expérience avec deux pièces, FP et PF ont chacun une pièce sur Pile et une pièce sur Face. Ainsi, on peut dire que FP et PF représentent deux réalisations possibles du tirage avec une pièce sur Pile et une pièce sur Face. En revanche, PP est la seule réalisation possible du tirage avec les deux pièces sur Pile, de même que FF est la seule réalisation possible du tirage avec les deux pièces sur Face.

Approfondissons la discussion avec l'exemple d'un jeu où l'on tire trois pièces. Tous les tirages possibles sont représentés sur l'illustration ci-dessous.

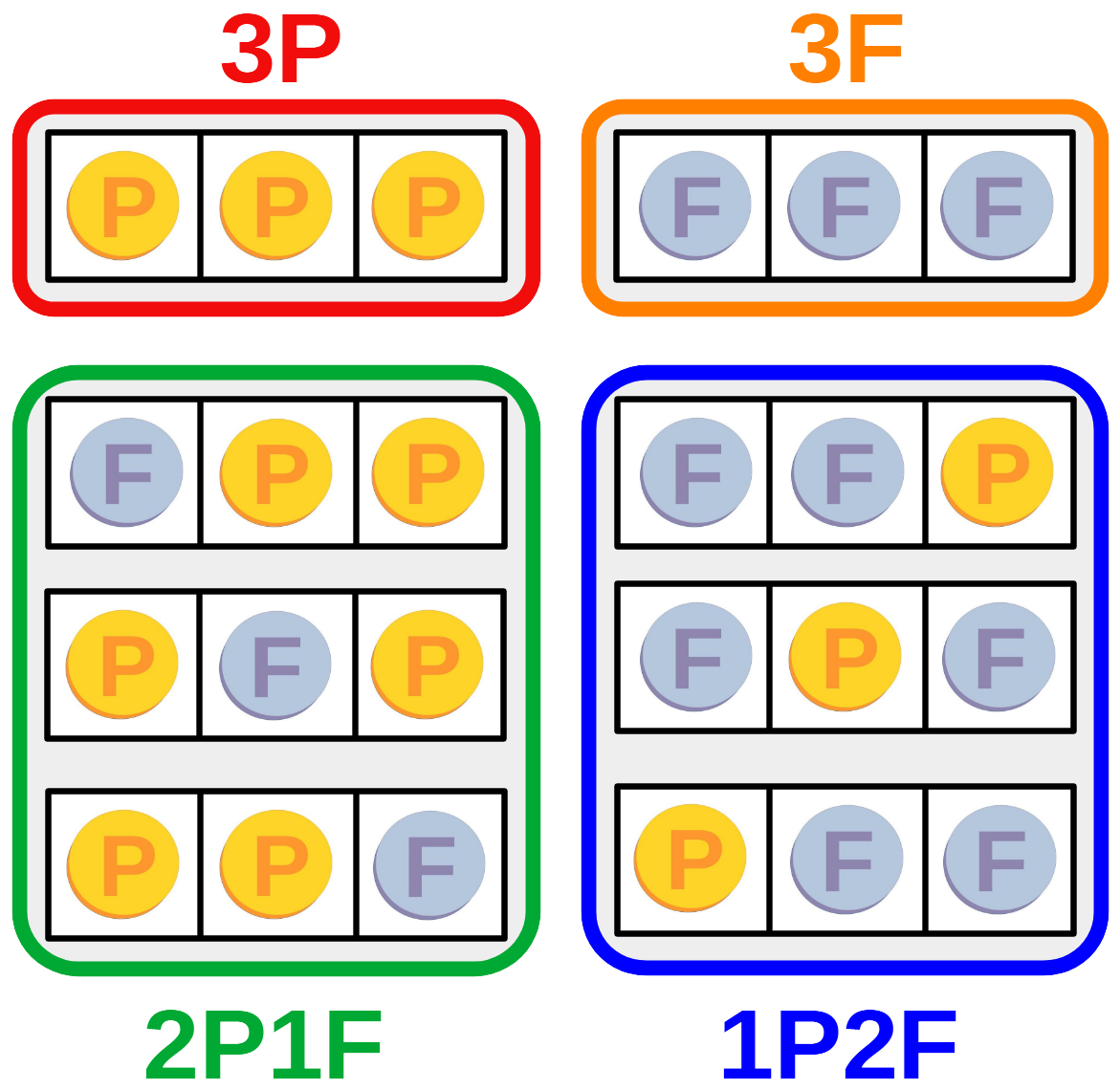
Là encore, on peut regrouper des arrangements pour donner une description globale des tirages qui peuvent être observés. On note alors qu'il existe trois tirages avec une pièce sur Pile et deux pièces sur Face. Ils sont entourés en bleu sur la figure. Il existe trois tirages, entourés en vert, avec deux pièces sur Pile et une pièce sur Face. En ce qui concerne les tirages avec les trois pièces identiques, trois Pile, entourés en rouge, ou trois Face, entourés en orange, ils sont chacun uniques.

Les arrangements qui donnent une description globale d'un groupe de tirages sont appelés des macro-états. Les arrangements qui décrivent les tirages de façon détaillée sont appelés des micro-états.

Par exemple, les tirages FPP, PFP et PPF sont trois micro-états. Ce sont trois micro-états du macro-état 2P1F avec deux pièces sur Pile et une pièce sur Face.

De manière générale, on dit qu'un macro-état possède un ou plusieurs micro-états.

Revenons aux tirages avec deux pièces. Les micro-états PF et FP sont les deux réalisations du macro-état avec une pièce sur Pile et une pièce sur Face noté 1P1F. Les trois macro-états du jeu à deux pièces sont : 2P pour deux fois Pile, 2F pour deux fois Face et 1P1F pour une fois Pile et une fois Face. Leurs probabilités respectives sont `1/4`, `1/4` et `1/2`, c'est-à-dire une chance sur quatre pour 2P et 2F, et une chance sur deux pour 1P1F.

La simulation avec 10000 tirages de deux pièces a été réanalysée mais cette fois en s'intéressant aux macro-états. Le graphique ci-dessous résume cette analyse en montrant le nombre de fois où chacun des trois macro-états 2F, 1P1F et 2P a été observé.

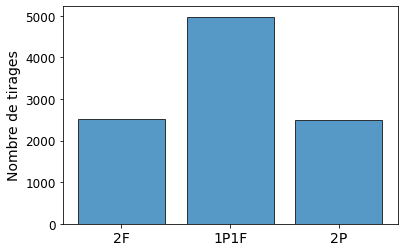
Comme l'indiquaient les probabilités mentionnées ci-dessus, c'est bien le macro-état avec une pièce Pile et une pièce Face qui est le plus observé et ce près de la moitié du temps (4979 fois pour la simulation présentée). Les combinaisons avec les deux pièces identiques 2P et 2F sont quant à elles observées un nombre similaire de fois, environ égale à 2500 chacune.

Jouons maintenant avec 4, puis 16 pièces par tirage, toujours en simulant 10000 tirages.

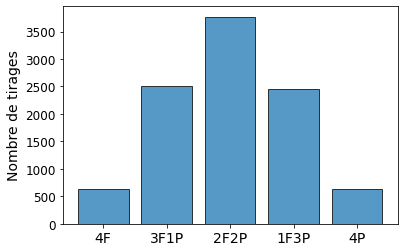
Dans le cas du jeu à 4 pièces, on peut remarquer ci-dessous que c'est l'arrangement avec deux fois Face et deux fois Pile (2F2P) qui est le plus observé.

Dans le cas du jeu à 16 pièces ci-dessous, c'est l'arrangement avec huit fois Face et huit fois Pile (8F8P) qui est le plus observé.

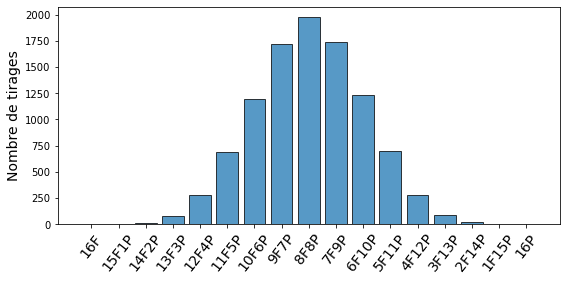
Si on réalisait des simulations avec un nombre encore plus grand de pièces, on trouverait encore que le macro-état le plus observé serait celui pour lequel le nombre de fois Pile est égal au nombre de fois Face (pour un nombre de pièces pair). Par exemple, avec 100 pièces, on trouverait que l'arrangement le plus probable serait 50 fois Face et 50 fois Pile (50F50P).

Résumons ce que le jeu Pile ou Face nous apprend.

• Pour chaque pièce, la probabilité de tirer Pile est toujours d'une chance sur deux. Il en va de même avec la probabilité de tirer Face.
• Quel que soit le nombre de pièces, tous les micro-états sont équiprobables avec la probabilité `1/2^n` où n est le nombre de pièces. Par exemple, dans un jeu à cinq pièces on n'a ni plus ni moins de chance de tirer PFPPP, PPFPP que de tirer FFFFF, concrètement, une chance sur `2^5` (2 puissance 5), soit une chance sur 32.
• Si on s'intéresse aux macro-états, le comportement de l'ensemble des pièces tirées au hasard devient bien plus prédictible car tous les macro-états ne sont pas équiprobables. En effet, le macro-état le plus probable aura autant de Pile que de Face. Par exemple, dans un jeu à 16 pièces, nos chances de gagner sont maximum en misant sur 8P8F alors qu'il est bien plus hasardeux de miser sur 16F ou même 14F2P.

On peut donc conclure que dans ce jeu de hasard, le macro-état avec autant de pièces tombées côté Pile que de pièces tombées côté Face a un statut bien particulier. C'est cet arrangement qui est le plus probable.

Avant de parler d'entropie, réfléchissons encore un peu sur le jeu de hasard Pile ou Face. Imaginons qu'on nous propose de jouer avec huit pièces. Pour gagner, on nous donne le choix de prédire le détail du tirage, ce qui nous rapporterait un gain maximum, ou bien de prédire combien de Pile et combien de Face seront observées, ce qui nous rapporterait un peu moins. Que vaut-il mieux faire ?

Concrètement se pose le problème de prédire quel micro-état précis va être tiré si on recherche un gain maximum, ou de prédire à quel macro-état le tirage appartiendra si on vise un gain moindre. Chaque micro-état a une probabilité de `1/256`. Donc si on mise par exemple sur FPFPFPFP, on a une chance sur 256 de gagner. Si on mise sur le macro-état le plus probable 4P4F, notre chance de succès est 70 fois plus grande avec 27,3%, soit plus d'une chance sur quatre. Est-ce qu'une probabilité de succès d'une chance sur quatre est suffisante pour se risquer ? Peut-être vaut-il simplement mieux ne pas jouer et garder son argent...

Et l'entropie dans tout ça ?

Quand on a bien compris ce que sont les micro-états et les macro-états, la définition de l'entropie est relativement simple. L'entropie mesure la variété de réalisations d'un macro-état en termes de ses micro-états. Toute la difficulté est de définir ce qu'on entend par micro-état et macro-état quand on s'intéresse à autre chose que Pile ou Face.

Reconsidérons le jeu à quatre pièces. Le macro-état 2P2F a le plus grand nombre de micro-états. Il a donc une entropie plus grande que tous les autres macro-états. On peut également noter que le macro-état le plus probable est celui qui a le plus grand nombre de micro-états. C'est donc le macro-état le plus probable qui a la plus grande entropie.

Reste à donner une formule pour calculer l'entropie. Comme l'a fait l'Autrichien Ludwig Boltzmann au XIXème siècle, désignons par W le nombre de micro-états d'un macro-état donné et par S l'entropie. La formule de Boltzmann `S = k ln W` permet de calculer l'entropie comme le produit du logarithme népérien de W (`ln W`) et de la constante de Boltzmann (`k`).

Prêts pour un test de compréhension ?

Pour renforcer notre compréhension de ce qui précède, intéressons-nous à un système de 20 jetons placés au hasard sur une grille de 10`times`10 cases, une case ne pouvant accueillir plus d'un jeton à la fois. Deux arrangements sont proposés ci-dessous.

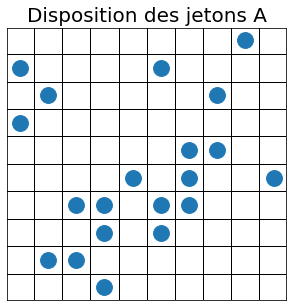
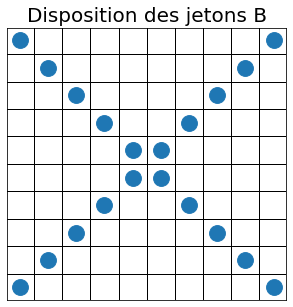
Question (piège) : Laquelle des dispositions A ou B a la plus grande entropie ?

Réponse : Ni l'une, ni l'autre. Les deux sont des micro-états d'un même macro-état. Pour obtenir l'entropie de ce macro-état il faut calculer le nombre de combinaisons correspondant au placement de 20 jetons dans 100 cases.

Question (difficile) : Partant du macro-état avec 20 jetons sur 100 cases, comment générer un macro-état avec une entropie plus grande ?

Indice : Remplir des cases avec des jetons est équivalent à arranger des jetons et des cases vides. Arranger des cases vides et des jetons, c'est très semblable à arranger des pièces côté Pile et des pièces côté Face.

Réponse : Comme l'indice le suggère calculer l'entropie du macro-état correspondant à 20 pièces sur 100 cases, c'est comme calculer l'entropie pour 20 pièces sur Pile et 80 pièces sur Face. Comme nous l'avons vu, le nombre de micro-états, et donc l'entropie, est maximum pour 50 pièces sur Pile et 50 pièces sur Face. Partant de 20 jetons, augmenter ce nombre génère un macro-état d'entropie plus grande. Nous ne devons cependant pas dépasser 79 jetons. Souvenez-vous des pièces. Le nombre de micro-états pour 80P20F est le même que pour 20P80F. Ainsi l'entropie pour 20 jetons est la même que pour 80. En conclusion, partant de 20 jetons, l'entropie augmentera en utilisant entre 21 et 79 jetons. Le maximum d'entropie étant obtenu avec 50 jetons.

Entropie et désordre

Il est fréquent de lire que l'entropie serait une mesure du désordre dans un système donné. Un exemple très qualitatif qui revient souvent est celui qu'une chambre d'enfant en désordre a une entropie plus grande que lorsqu'elle est rangée. La discussion ci-dessus devrait nous avoir armés pour comprendre ce qui est incorrect dans de telles affirmations.

Reprenons les dispositions de jetons du paragraphe précédent. Nous pourrions dire que la disposition A est en désordre au contraire de la disposition B dont le motif est très structuré. Toutefois nous savons maintenant que ni la disposition A, ni la disposition B n'ont d'entropie. Ce sont deux micro-états possibles de 20 jetons dans une grille de 100 cases. Qui plus est, elles sont équiprobables si elles sont générées au hasard.

Revenons à la chambre d'enfant. Voyez-vous pourquoi elle n'a pas moins d'entropie quand elle est rangée que lorsqu'elle est en désordre ? La configuration "chambre rangée" est un micro-état du même macro-état que toutes celles jugées en désordre. On peut calculer l'entropie de la chambre avec un certain nombre d'objets et un certain nombre d'emplacements où les ranger, mais pour un nombre d'objets et d'emplacements donnés, qu'elle soit rangée ou en désordre ne change pas son entropie.

On le voit, penser à l'entropie en termes de mesure du désordre n'est pas adapté. En adoptant ce point de vue, on se force à réfléchir en termes de combinaison unique, de micro-état unique, alors que l'entropie mesure la variété de micro-états pour un arrangement global donné.

Si vous aimez le calcul...

Lançons quatre pièces au hasard, comment sait-on que 2F2P a le plus grand nombre de micro-états que l'on peut obtenir avec ces quatre pièces ? De manière plus générale, si on joue avec n pièces, si k pièces tombent côté Pile, combien de micro-états correspondent à kP(n-k)F ?

En langage mathématique, nous recherchons le nombre de combinaisons de k éléments dans un ensemble de n éléments avec `k>=n`. Ce nombre est `C_n^k = {n!} / {k!(n-k)!}`.

Pour le jeu à quatre pièces, le tableau ci-dessous donne les valeurs du nombre de micro-états pour chaque macro-état possible. Le lecteur averti remarquera que ces nombres sont ceux du triangle de Pascal pour n=4.

Macro-état	Nombre de micro-états
4P	`C_4^0 = 1`
3P1F	`C_4^1 = 4`
2P2F	`C_4^2 = 6`
1P3F	`C_4^3 = 4`
4F	`C_4^4 = 1`

On constate bien que pour quatre pièces, le nombre de micro-états maximum est obtenu avec deux pièces côté Pile et deux pièces côté Face (2P2F).

Comment démontrer que dans le cas général où n pièces (n pair) sont jetées c'est le macro-état avec `n/2` pièces sur Pile qui a le plus grand nombre de micro-états ? Il s'agit de rechercher la valeur de k pour laquelle `C_n^k` est maximum et de montrer que ce maximum est unique. Cela requiert plusieurs lignes de calcul et un peu de temps. A vos crayons !

Question : Une simulation place des jetons au hasard sur une grille de 16 cases. De combien augmente l'entropie en passant de trois à huit jetons ?

Réponse : Avec trois jetons, l'entropie est proportionnelle à `ln C_16^3 = ln 560`. Avec huit jetons elle est proportionnelle à `ln C_16^8 = ln 12870`. En passant de trois jetons à huit jetons, l'entropie a été multipliée par environ 1,5.

Question : Une simulation place au hasard 4 jetons sur une grille de 16 cases. Quelle est la probabilité d'obtenir un jeton à chaque coin ? La probabilité d'obtenir les quatre jetons au centre ?

Réponse : Les deux dipositions "un jeton dans chaque coin" et "tous les jetons au centre" sont équiprobables. Le nombre de combinaisons qui correspondent à quatre jetons sur 16 cases est `C_16^4 = (16!)/(4!12!) = 1820`. La probabilité d'obtenir l'une des dispositions est donc `1/C_16^4`, soit une chance sur 1820.

Question : Jouons à Pile ou Face avec 16 pièces. Quelle est la probabilité d'obtenir 15P1F? Quelle est la probabilité d'obtenir 8P8F ?

Réponse : Le nombre total de combinaisons possibles avec 16 pièces est `2^16 = 65536`. La probabilité d'obtenir 15P1F est `C_16^1 / 2^16 = 16/65536 approx 0,024%`. La probabilité d'obtenir 8P8F est `C_16^8 / 2^16 = 12870/65536 approx 20%`, soit environ 10000 fois plus que la probabilité d'obtenir 15P1F.